Heap

2월 4주차 스터디 발표 자료📖
이번 주에 정리할 알고리즘은 Heap입니다!!

힙 (Heap)

---

• 데이터에서 최댓값과 최솟값을 빠르게 구하기 위해 고안된 완전 이진 트리이다.
• 키값의 대소관계는 오로지 부모노드와 자식노드 간에만 성립하며, 형제 사이에는 대소관계가 정해지지 않는 느슨한 정렬 상태
• 이진 탐색트리와는 달리 중복 값을 허용한다.
• 우선순위 큐, 힙 정렬 등에서 사용한다.
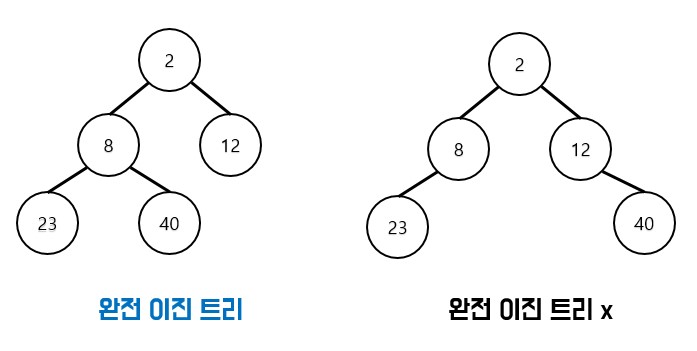
• 🤔 완전 이진 트리?
  • 마지막 레벨을 제외하고 모든 레벨이 완전히 채워져있다.
  • 마지막 레벨이 꽉 차 있지 않아도, 노드가 왼쪽에서 오른쪽으로 채워져야한다.
  • 완전 이진 트리는 배열을 사용해 효율적으로 표현이 가능하다.

힙의 종류?

---

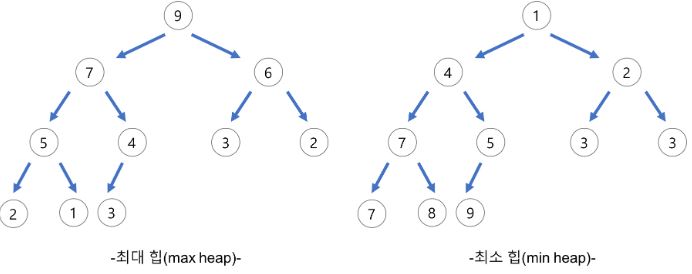
1. 최대힙 (Max Heap)
   • 부모 노드의 키 값이 자식 노드의 키 값보다 크거나 같은 완전 이진 트리
   • key(부모 노드) >= key(자식 노드)
2. 최소힙 (Min Heap)
   • 부모 노드의 키 값이 자식 노드의 키 값보다 작거나 같은 완전 이진 트리
   • key(부모 노드) <= key(자식 노드)

힙의 구현?

---

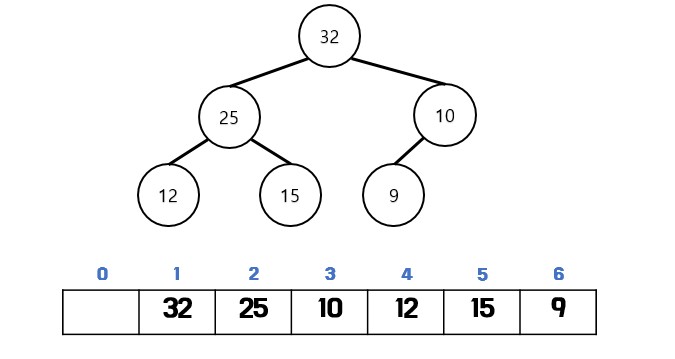
• 힙은 배열로 구현된다.
• 왼쪽 자식의 인덱스 = [부모 인덱스] x 2
• 오른쪽 자식의 인덱스 = [부모 인덱스] x 2 + 1
• 부모 인덱스 = [자식 인덱스] / 2

힙의 삽입

• 그림은 최대 힙이라고 가정한다.
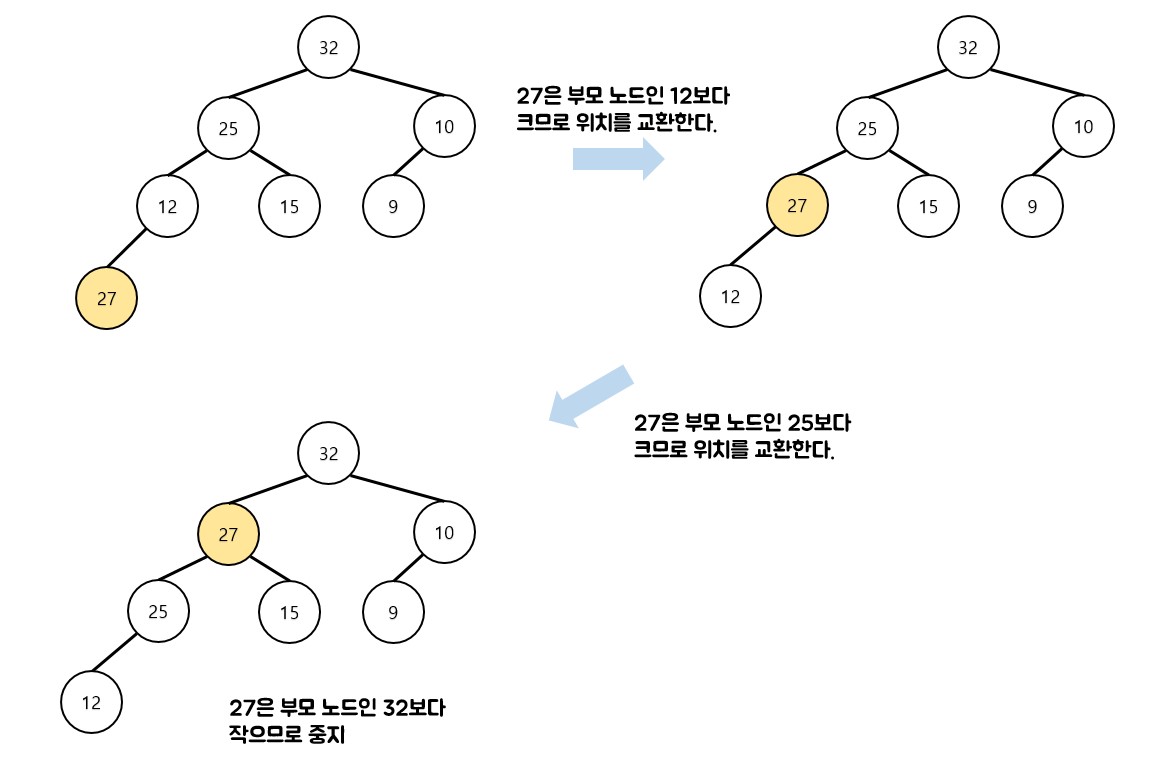
  1. 새로운 노드는 항상 힙의 맨 끝에 추가된다.
  2. 자신의 부모 노드와 값을 비교하여 부모 노드의 값이 자신보다 작다면 위치를 바꾼다.
  3. 자신보다 크거나 같은 값을 가진 부모 노드를 만나거나, 루트에 도달할 때까지 반복한다.

힙의 삭제

• 그림은 최대 힙이라고 가정한다.
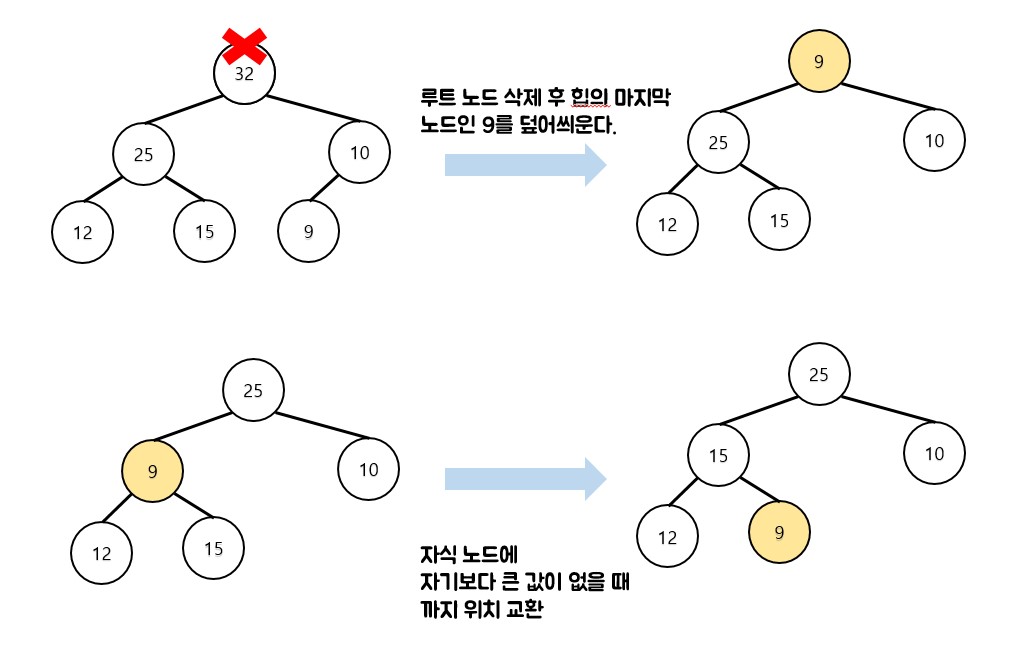
  1. 힙에서 삭제되어야 하는 원소는 루트이다.
  2. 힙의 마지막 노드를 루트에 덮어 씌운다.
  3. 힙의 대소 관계 조건을 만족시킬 때까지 노드를 이동한다.

힙을 활용해 문제를 풀어보자!

---

1. 프로그래머스 - 더 맵게

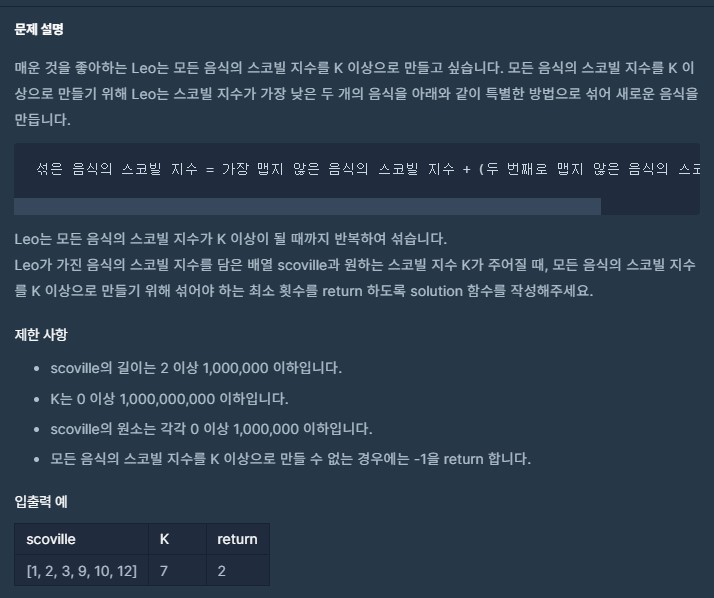
• 우선순위 큐(Priority Queue)?
  • 우선순위 큐는 들어간 순서에 상관없이 우선순위가 높은 데이터가 먼저 나오는 구조이다.
  • 우선순위 큐는 힙(Heap)이라는 자료구조를 가지고 구현할 수 있다.
• 접근 방법?
  1. 모든 음식의 스코빌 지수가 k 이상이려면 최소 값이 k이상이면 된다.
  2. 최소값에 관련된 문제이므로, 우선순위 큐 중에서 최소힙을 활용하자!
  3. 우선순위 큐(최소 힙)는 우선 순위가 높은 순으로 정렬되있다. 즉, 오름차순
  4. 우선순위 큐에서 값 2개를 가져온다.
  5. 해당 값을 주어진 식에 대입하고 결과 값을 우선순위 큐에 추가한다.
  6. 우선순위 큐의 최상단 값이(최소 값) k 이상인지 확인한다
  7. 값이 k 이상이면 종료, k 미만이면 4-6과정을 반복한다.

    import java.util.*;
  
    class Solution {
        public int solution(int[] scoville, int K) {
            int answer = 0;
  
            // 최소 값이 우선순위인 큐 = 최소 힙
            // 최대 값이 우선순위인 큐 = 최대 힙 new PriorityQueue<>(Collections.reverseOrder());
            PriorityQueue<Integer> minHeap = new PriorityQueue<Integer>();
            for(int n : scoville) minHeap.add(n);
              
            while(minHeap.peek() < K){
                int min1 = minHeap.poll();
                int min2 = minHeap.poll();
                  
                minHeap.add(min1 + min2 * 2);
                answer++;
                  
                if(minHeap.peek() >= K) break;
                if(minHeap.peek() < K && minHeap.size()==1){
                    answer = -1;
                    break;
                }
            }
            return answer;
        }
    }
  

2. 프로그래머스 - 디스크 컨트롤러

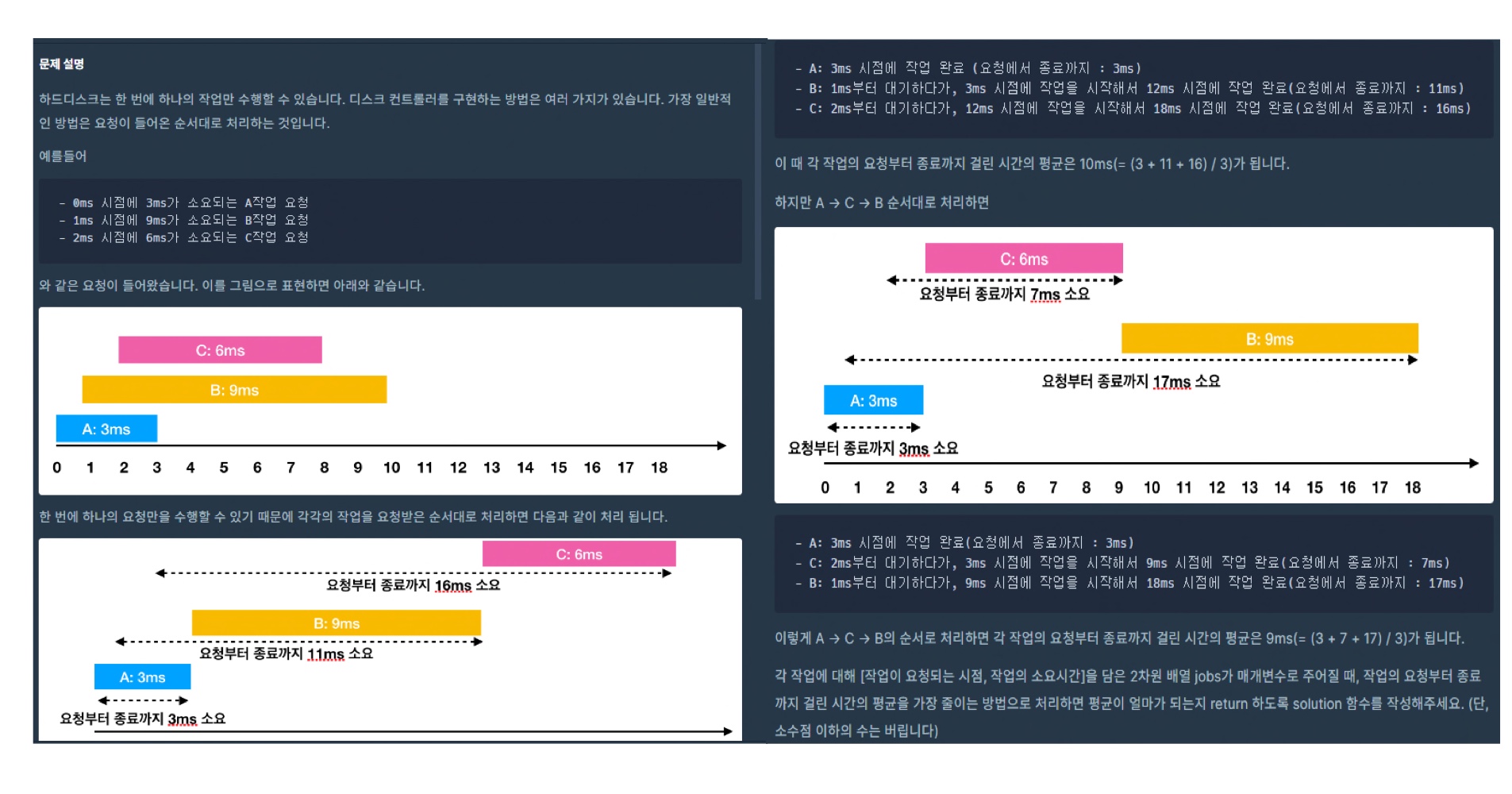
• 접근 방법?
  1. 요청 시간부터 종료시간의 평균을 줄이려면 소요시간이 작은 작업부터 처리해야한다.
  2. 단, 소요시간이 작은 작업부터 무작정 실행하면 안된다. 요청 시간 1000초에 작업 시간 1초일수도 있기 때문..
  3. 요청시간이 제일 빠른 작업부터 실행하고, 해당 작업이 끝났을 시점에 실행 가능한 작업 중 소요시간이 작은 작업을 실행해야한다.
  4. 작업을 완료했을 때 제일 빠른 작업이 현재 시간 이후라면 해당 시간으로 바로 이동한다.

    import java.util.*;
  
    class Solution {
        public int solution(int[][] jobs) {
            int answer = 0;
  
            //jobs[][1](소요시간 기준) 오름차순 정렬
            PriorityQueue<int[]> minHeap = new PriorityQueue<int[]>((o1,o2) -> (o1[1]-o2[1])); 
            //jobs[][0](요청시간 기준) 오름차순 정렬
            Arrays.sort(jobs, (o1,o2) -> (o1[0]-o2[0])); 
  
            int index = 0;
            int time = jobs[0][0]; // 현재 시간
  
            while(index < jobs.length || !minHeap.isEmpty()){
                while(index < jobs.length && jobs[index][0] <= time){ // 남아있는 작업이 있어야하며, 요청시간이 현재 시간보다 적어야함
                    minHeap.add(jobs[index]); // 위의 조건을 충족하면 작업 대기
                    index++;
                }
                if(minHeap.isEmpty()){
                    //현재 시간이 이후 작업 요청시간 전일 때
                    time = jobs[index][0]; // 제일 빠른 요청시간으로 시간대 옮기기
                }
                if(!minHeap.isEmpty()){ // 해야 할 작업이 있다면
                    int[] job = minHeap.poll(); // 해당 작업 가져오기
                    answer += time - job[0] + job [1]; // 대기 시간과 작업량 더하기
                    time += job[1];
                }
            }
  
            return answer/jobs.length;
        }
    }