그리디 알고리즘

알고리즘 한번 싹 정리할 겸 Greedy에 대해 정리하고자 합니다!
Greedy도 그렇고.. 완전탐색도 그렇고.. 알고리즘은 해도해도 끝이 없네요🥲
열심히 해봅시다!!!!

탐욕법 (Greedy)

---

• 현재 상황에서 가장 최선의 선택을 고르는 알고리즘
• 하지만 그리디 알고리즘은 최적 값을 언제나 항상 고를 수 있는 것은 아니다.
  현재 상황에서의 최선의 선택이 모든 경우의 수의 최적의 해라고 보장할 수 없다.

Greedy를 사용하기 위한 조건?

1. 탐욕 선택 속성 (greedy choice property)
   각각의 선택이 다른 선택에 영향을 주지 않을 것
2. 최적 부분 구조 (optimal substructure)
   전체 문제의 최적 해결 방법은 부분 문제에 대한 최적 해결방법이다.

Greedy로 문제를 풀지 못하는 경우?

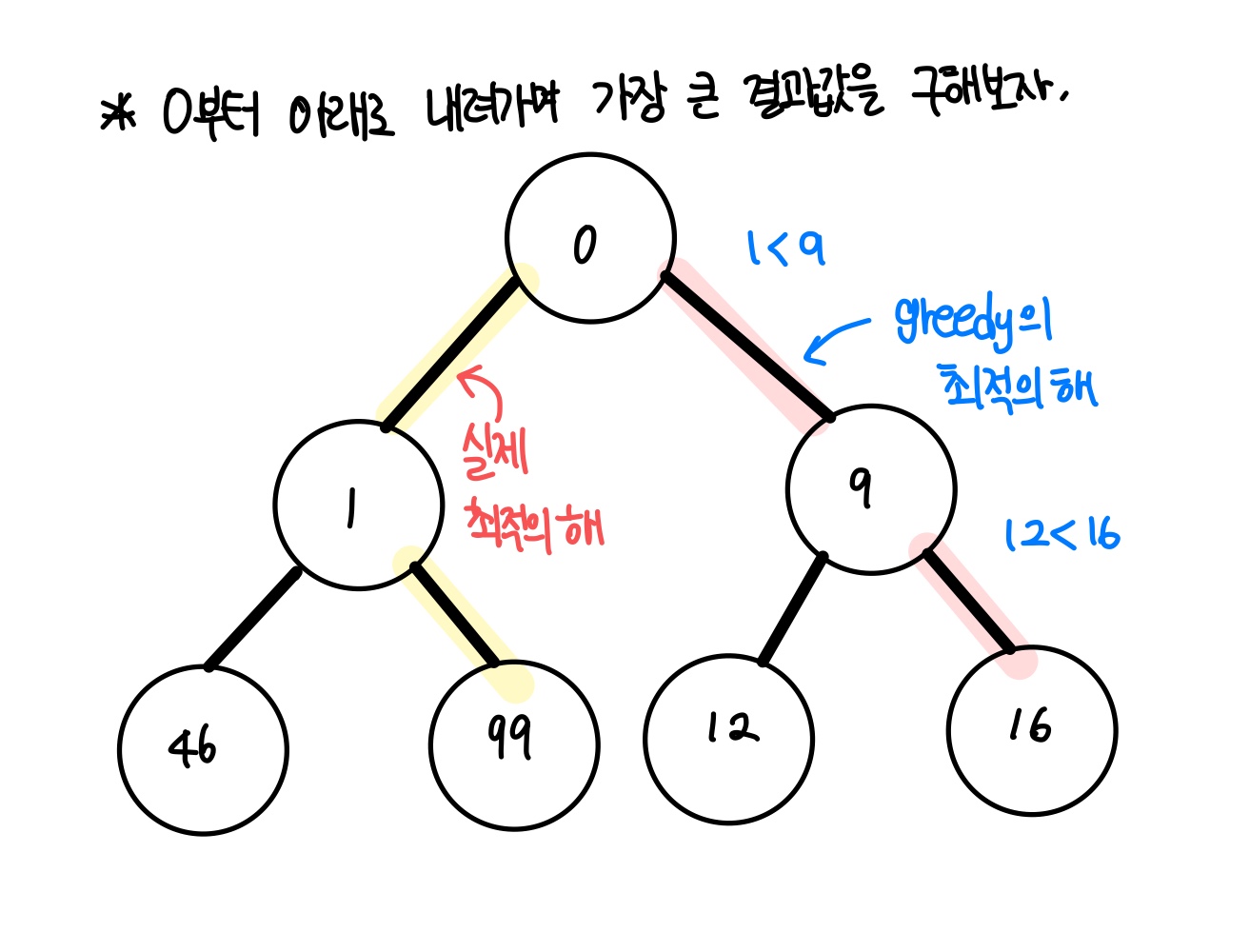
• greedy 알고리즘은 단순히 1과 9중에 9가 크니까 9를 선택하고, 12와 16중 16이 크니까 16을 선택할 것이다.
• 하지만 최선의 선택은 0 - 1 - 99를 선택하는 것이다. 따라서 그리디의 해답이 모든 경우에 대한 최적의 해라고 할 수 없다.

Greedy 문제를 실제로 풀어보자!

---

1. 백준 11047 - 동전 0

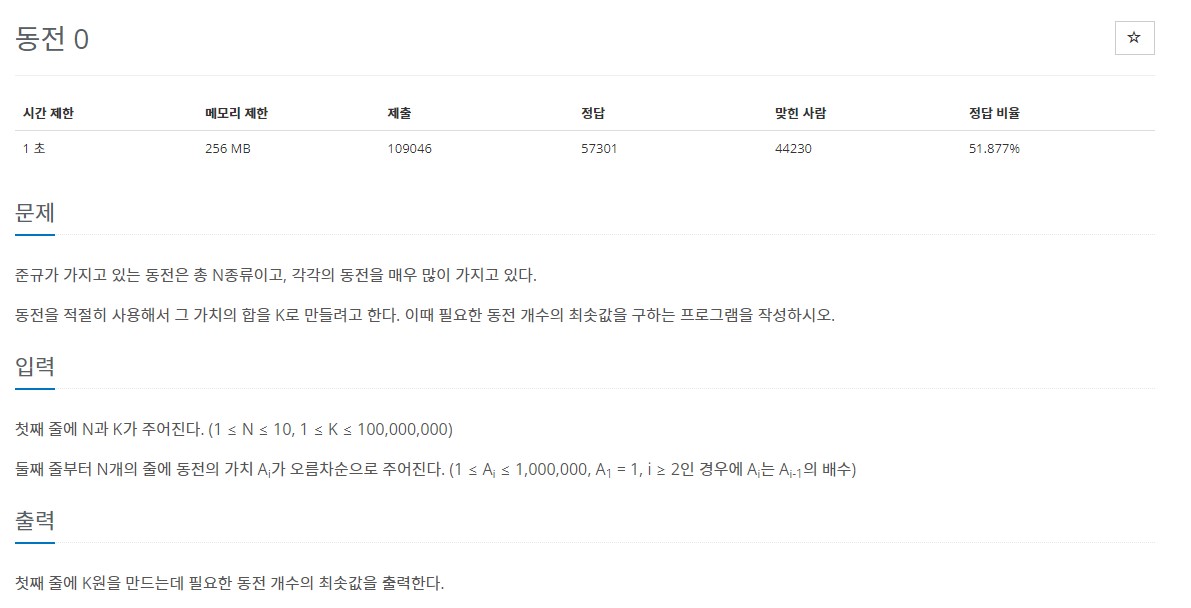
• 접근 방법
  • 동전 개수의 최소로 원하는 금액을 만들자!
  • 금액이 큰 동전부터 할당하면 최소의 개수가 나오지않을까?
  • 큰 금액부터 할당하는 경우만큼 다른 경우에서도 적은 수의 동전이 나오지 않는다.

    import java.util.Scanner;
  
    public class p11047 {
  
        public static void main(String[] args) {
            Scanner sc = new Scanner(System.in);
              
            int n = sc.nextInt();
            int k = sc.nextInt();
            int[] coins = new int[n];
              
            for(int i=0;i<n;i++) {
                coins[i] = sc.nextInt();
            }
              
            int answer = 0;
              
            for(int i=n-1;i>=0;i--) {
                int count = k / coins[i];
                k -= (count * coins[i]);
                answer += count;
                if(k==0) break;
            }
              
            System.out.println(answer);
  
        }
  
    }
  

• 그럼 동전 문제는 전부 그리디로 풀 수 있을까?
  • 동전이 10원 30원 40원 50원이 있다고 가정해보자. 70원을 만들 때 50원 부터 할당하는 것이 맞을까?
    
    • 이런 경우는 그리디로 푸는 것이 최선의 답이 아니다.
      30원과 40원 단 두개의 동전을 할당하는 것이 가능하기 때문에 현재 상황에서의 최적의 해가 전체 경우의 최적의 해가 아니다. 즉, 상황을 판별할 줄 알아야한다.
    • 동전 문제는 큰 액수가 작은 액수의 배수여야한다는 조건이 붙는다고 생각하면 된다.

2. 백준 2875 - 대회 or 인턴

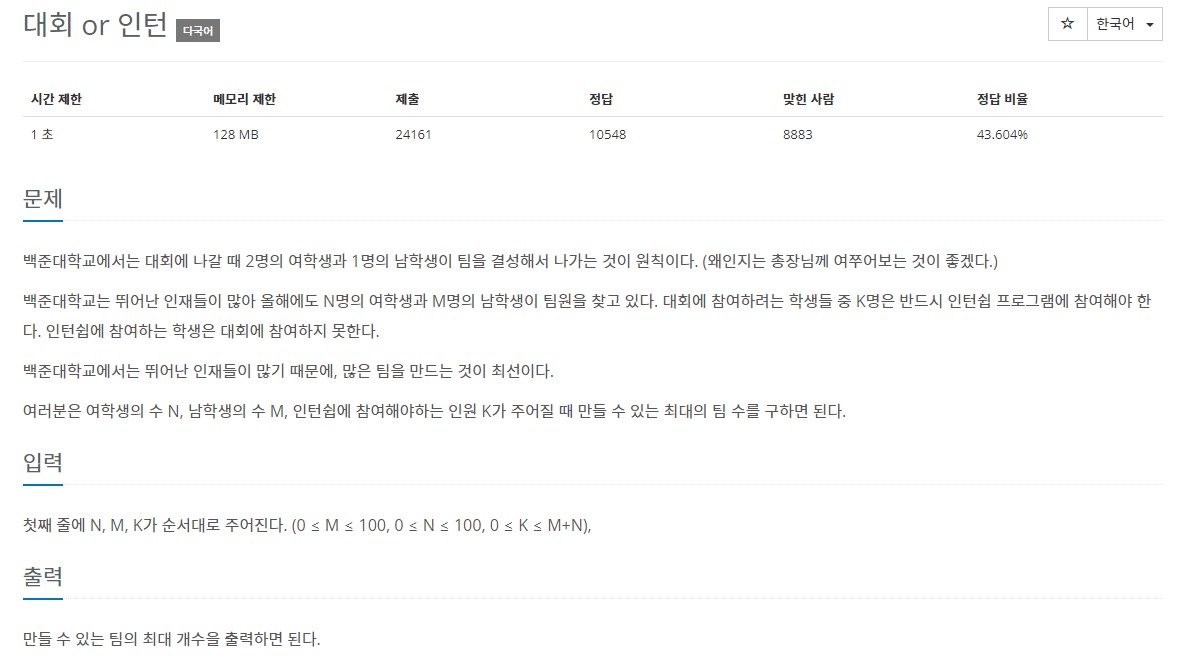
• 접근 방법
  • 여학생과 남학생 각각 만들 수 있는 팀의 개수를 구한다.
  • 둘 중 더 작은 개수의 팀이 만들 수 있는 최대 팀의 개수
  • 인턴쉽은 단순히 최대로 가능한 팀의 인원을 빼고 k명이 남는지 확인한다.
    • k명이 남거나 그 이상 남는다면 성공
    • k명 미만이라면 팀을 줄이면된다.

    import java.util.Scanner;
    public class p2875 {
  
        public static void main(String[] args) {
            Scanner sc = new Scanner(System.in);
              
            int n = sc.nextInt(); // 여학생
            int m = sc.nextInt(); // 남학생
            int k = sc.nextInt(); // k명은 인턴쉽 참여해야함
              
            // 만들 수 있는 팀 수
            int teams = Math.min(n/2,m);
            while(true) {
                if(n+m - 3*teams >= k) break;
                else teams -= 1; // 인턴쉽으로 갈 수 있는 인원이 k명 미만이라면 team을 줄인다.
            }
              
            System.out.println(teams);
        }
  
    }
  

3. 백준 10610 - 30

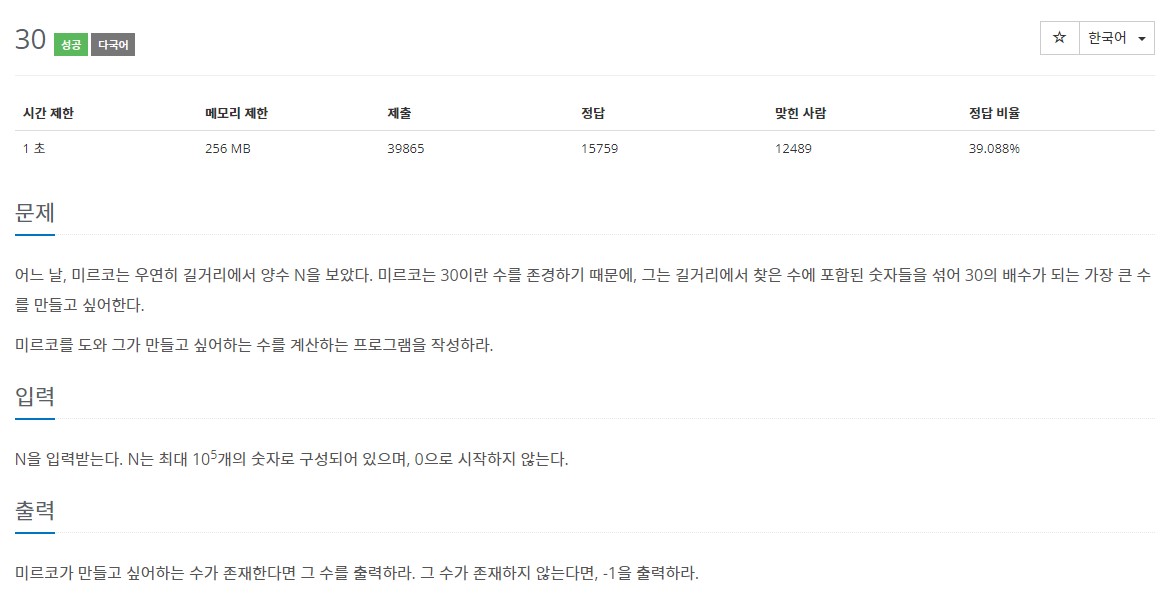
• 접근 방법
  • 주어진 수를 섞어 가능한 30의 배수 중 가장 큰 값을 찾자
  • 일단 주어진 수를 정렬한다.
  • 내림차순으로 정렬한 수가 조합에서 가능한 제일 큰 수. 따라서 해당 값이 30의 배수인지 확인해본다.
    • 끝자리가 0으로 끝나는가?
    • 끝자리를 제외한 앞자리의 합이 3의 배수인가?

      import java.util.Arrays;
      import java.util.Scanner;
    
      public class p10610 {
    
          public static void main(String[] args) {
              Scanner sc = new Scanner(System.in);
              String n = sc.next();
              char[] number = n.toCharArray();
              Arrays.sort(number);
                    
              int sum = 0;
                    
              StringBuilder sb = new StringBuilder();
              for(int i= number.length-1; i>=0; i--) {
                  int num = number[i] - '0';
                  sum += num;
                  sb.append(num);
              }
                    
              // 30의 배수인가? 끝이 0으로 끝날 것, 나머지 자리 수를 다 더했을 때 3의 배수일 것
                    
              if(sum % 3 == 0 && number[0]=='0') {
                  System.out.println(sb.toString());
              }else {
                  System.out.println(-1);
              }
          }
    
      }