이분탐색 (BinarySearch)

2월 3주차 스터디 발표 자료📖
3주차 기술면접 주제 중 두번 째 주제입니다!
이분탐색에 대해 정리하고자 합니다.

이분탐색 (이진탐색)

---

• 배열의 중앙 값을 조사하여 찾고자 하는 항목이 왼쪽 또는 오른쪽에 있는지 확인하는 방식
• 찾고자 하는 항목의 방향이 정해지면 반대 방향은 탐색할 필요가 없기 때문에, 매 단계마다 탐색의 범위를 반 씩 줄일 수 있음
• 정렬된 배열에서 사용하기 적합한 탐색 방법
• 탐색 시간은 O(log n)

이분탐색 방법

---

1. 정렬된 배열 array[]가 있고, 범위는 low~high로 설정한다.
2. low와 high 값으로 mid 값을 설정한다. mid = (low + high) / 2
3. array[mid]의 값과 찾고자 하는 값(value)을 비교한다.
   • value > array[mid] : low를 mid+1로 설정한다.(오른쪽)
   • value < array[mid] : high를 mid-1로 설정한다.(왼쪽)
   • value == array[mid] : 값을 찾았으므로 array[mid]값을 리턴한다.
4. low가 high가 될 때까지 위 단계를 반복한다.

이분탐색을 실제로 풀어보자!

---

1. 프로그래머스 - 입국심사

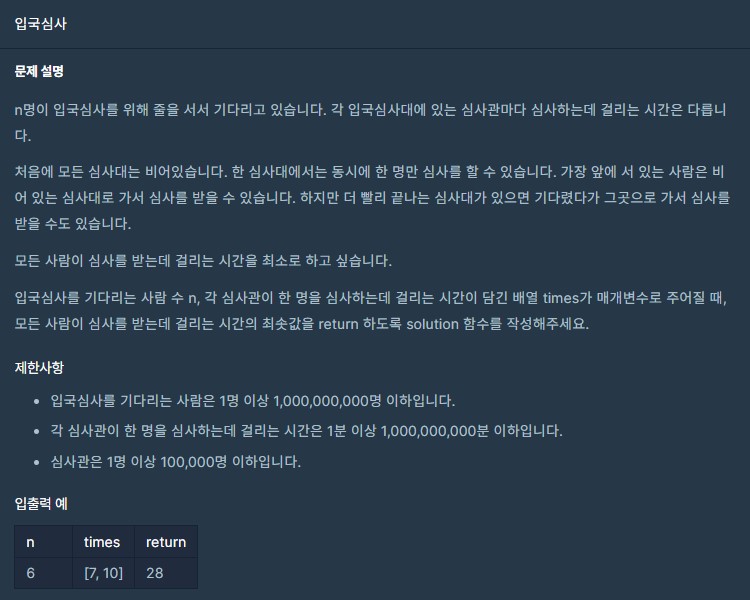
• 접근 방법?
  1. 입국심사의 최소 시간은 times[0]로 설정한다. 최소 시간은 1초가 아닌 적어도 times[0]초 일것이다.
  2. 입국심사의 최대 시간은 모든 사람이 가장 오래걸리는 입국 심사관에서 심사를 하는 것이다.
  3. 최소시간 ~ 최대시간의 범위 내에 우리가 찾고자 하는 값이 있을 것이다! 이분탐색 시작
  4. mid 시간 중 n명을 처리할 수 있는 mid 시간을 구하고, 해당 시간 중에서 가장 적은 값이 우리가 원하는 값이다.

import java.util.*;
class Solution {
    public long solution(int n, int[] times) {
        long answer = 0;

        Arrays.sort(times);  
        long low = (long) times[0]; // 입국 심사 최소 시간
        long high = (long) times[times.length - 1] * n; // 입국심사 최대 시간

        while(high>=low){
            long sum = 0;
            long mid = (low + high) / 2; 

            // mid 시간 내에 입국 심사가 가능한 최대 인원 수
            for(int time : times){
                sum += mid / time; 
            }

            if(sum < n) { // n명보다 적게 처리 (시간이 더 필요함)
                low = mid + 1;
            }else { // n명보다 많이 처리 (걸리는 시간을 줄여 최소 시간 구하기)
                high = mid - 1; 
                answer = mid;
            }
        }
        return answer;
    }
}

2. 백준 1654번 - 랜선 자르기

• 접근 방법?
  1. 막대의 최대 길이는 주어진 막대의 최대 길이라 가정한다.
  2. 자를 수 있는 막대의 최대 길이는 최소길이 ~ 최대길이 범위에 존재할 것이다.
  3. mid 값으로 잘랐을 때 막대의 길이가 n개 이상이라면 길이를 더 늘린다.
  4. mid 값으로 잘랐을 때 막대의 길이가 n개 미만이라면 길이를 줄인다.
  5. 가능한 mid값 중 최대 값이 구하고자 하는 값이다.

import java.util.Scanner;

public class p1654 {
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		int k = sc.nextInt();
		int n = sc.nextInt();
		long target = 0;
		
		int[] list = new int[k];
		for(int i=0;i<k;i++) {
			list[i] = sc.nextInt();
			target = Math.max(list[i], target);
		}
		
		long low = 1;
		long high = target;
		long max = 0;
		
		while(high >= low) {
			long mid = (low+high)/2;
			long total = 0;
			
			for(int len :list) {
				total += (len / mid); // 만들 수 있는 막대기의 최대 개수
			}
			
			if(total < n) { // 가능한 막대기의 개수가 n개보다 작다면 길이를 줄인다.
				high = mid - 1;
			}else { // 가능한 막대기의 개수가 n개보다 많다면 길이를 늘리자. ( 최대값을 구할거니까 )
				low = mid + 1;
				max = Math.max(max,mid);
			}
		}
		System.out.println(max);
	}
}

3. 백준 2805번 - 나무 자르기

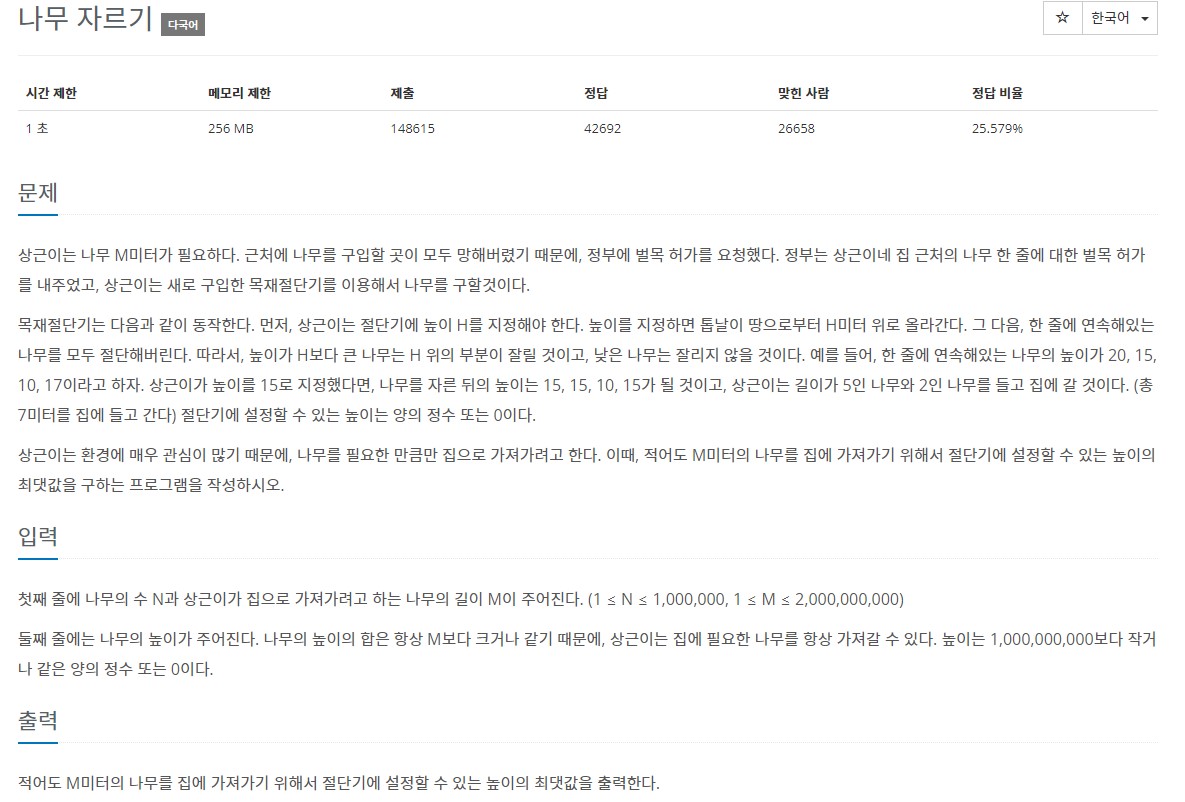
• 접근 방법?
  1. 톱날 높이의 최대 값이 가장 긴 나무의 길이라 가정한다.
  2. 톱날 높이의 최대 값은 최소길이 ~ 최대길이 범위에 존재할 것이다.
  3. mid 값으로 잘랐을 때 잘려진 나무의 길이가 M 이상이라면 길이를 더 늘린다.
  4. mid 값으로 잘랐을 때 잘려진 나무의 길이가 M 미만이라면 길이를 줄인다.
  5. 가능한 mid값 중 최대 값이 구하고자 하는 값이다.

import java.util.Arrays;
import java.util.Scanner;

public class p2805 {
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		int n = sc.nextInt();
		int m = sc.nextInt();
		long max = 0;
		
		int[] list = new int[n];
		for(int i=0;i<n;i++) {
			list[i] = sc.nextInt();
			max = Math.max(max, list[i]);
		}

		Arrays.sort(list); // 나무 길이 정렬
		
		long low = 1;
		long high = max;
		
		while(high >= low) {
			long mid = (low+high)/2;
			long sum = 0;
			
			for(int len : list) {
				if(len > mid) { // 나무의 길이가 자르는 길이보다 높다면
					sum += len-mid; // 나무가 잘린다.
				}
			}
			
			if(sum < m) { //자른 나무의 길이 합이 m 보다 작으면
				high = mid - 1;
			}else { // 자른 나무의 길이 합이 m보다 크거나 같으면
				low = mid + 1; 
			}
		}
		System.out.println(high);
	}
}